Các phương pháp tìm nguyên hàm
Đổi biến đổi số là 1 trong những phương pháp tính nguyên hàm được áp dụng thường xuyên, phía trên là phương thức hiệu quả để lấy bài toán nguyên hàm dạng phức tạp thành những bài toán nguyên hàm cơ bản.
Bạn đang xem: Các phương pháp tìm nguyên hàm
Vậy cách tính nguyên hàm bằng cách thức đổi biến số cụ thể như gắng nào? được áp dụng để tính nguyên hàm của hàm vô tỉ, hàm hữu tỉ, hay hàm vị giác,... , chúng ta hãy cùng tò mò qua nội dung bài viết dưới đây, đồng thời vận dụng phương thức này nhằm giải một số trong những bài tập tìm nguyên hàm.
I. Phương pháp nguyên hàm
* cách làm nguyên hàm cơ phiên bản (hàm vô tỉ, hữu tỉ, hàm mũ, hàm e, lượng chất giác)
1.
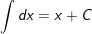
2.
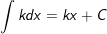
3.
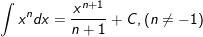
4.
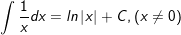
5.
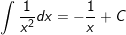
6.
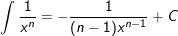
7.
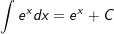
8.
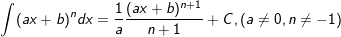
15.
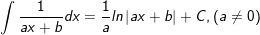
16.
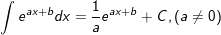
17.
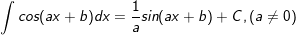
18.
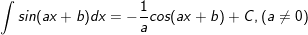
19.
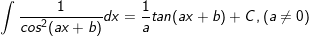
20.
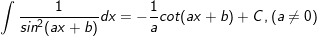
21.
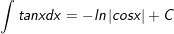
22.
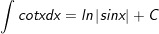
23.
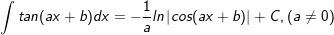
24.

* bí quyết nguyên hàm nâng cao (hàm hữu tỉ, hàm căn, hàm mũ e, hàm vị giác)
25.
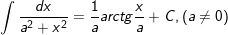
26.
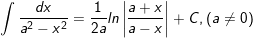
27.
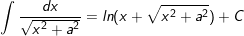
28.
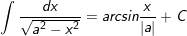
29.
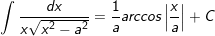
30.
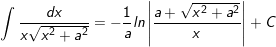
31.
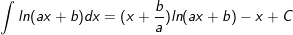
32
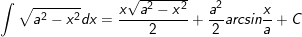
33.
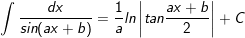
34.
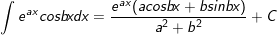
35.
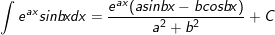
II. Phương pháp tính nguyên hàm bằng phương pháp đổi vươn lên là số
- phương pháp đổi phát triển thành số để xác minh nguyên hàm tất cả hai dạng dựa trên định lý sau:
a) Nếu
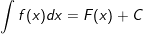

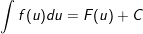
b) nếu như hàm số f(x) liên tục thì khi để x = φ(t) trong những số đó φ(t) với đạo hàm của nó φ"(t) là đều hàm số liên tục, ta đang được:
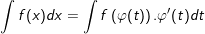
- Từ kia ta trình bày hai việc về phương thức đổi trở thành (phép đổi khác 1 thì x là hàm theo t, phép đổi khác 2 thì t là hàm theo x) ví dụ như sau:
* bài toán 1: Sử dụng phương thức đổi biến chuyển số dạng 1 tìm kiếm nguyên hàm I = ∫f(x)dx
* Phương pháp:
- Ta tiến hành theo những bước:
+ bước 1: lựa chọn x = φ(t), trong đó φ(t) là hàm số mà lại ta chọn cho thích hợp.
+ cách 2: mang vi phân 2 vế, dx = φ"(t)dt.
Xem thêm: Giá Xe Dream Việt Mới 2020, Tìm Hiểu Các Đời Xe Dream Việt Từ Năm 2012
+ cách 3: bộc lộ f(x)dx theo t và dt: f(x)dx = f<φ(t)>.φ"(t)dt = g(t)dt.
+ cách 4: lúc ấy I = ∫g(t)dt = G(t) + C
* lưu ý: các dấu hiệu dẫn tới vấn đề lựa chọn ẩn phụ vẻ bên ngoài trên thông thường là:
+ Dấu hiệu
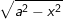
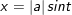
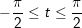
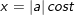
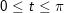
+ Dấu hiệu
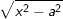
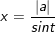
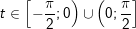
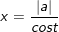
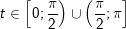
+ Dấu hiệu
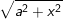
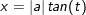
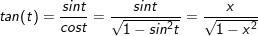
Ví dụ 2: Tính tích phân bất định
* Lời giải:
- Ta có, x2 + 2x + 3 = x2 + 2x + 1 + 2 = (x+1)2 + (√2)2 nên
Đặt: x + 1 = √2tan(t).
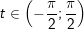
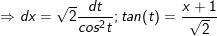
- Ta có:
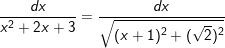

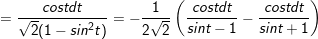
- lúc đó:
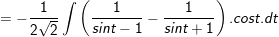
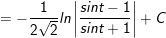
- Mà
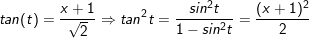
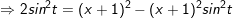
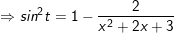
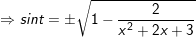
Ví dụ 3: Tính tích phân cô động sau:
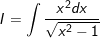
* Lời giải:
- ĐK: x2 - 1 >0 ⇔ x > 1 hoặc x 1
- Đặt
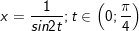
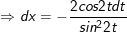
- cần có:
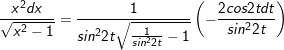
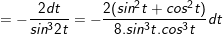
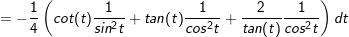
⇒
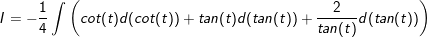
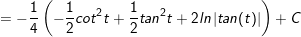
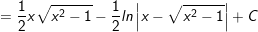
+ TH2: x * Lời giải:
- Đặt
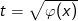
+ vết hiệu 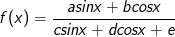
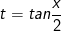
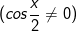
+ dấu hiệu 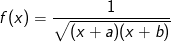
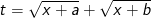
- Đặt
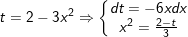
- khi đó,
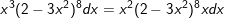
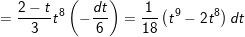
⇒
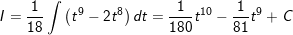
Ví dụ 2: Tính tích phân cô động sau:
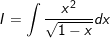
* Lời giải:
- Đặt
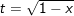
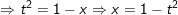
- khi đó:
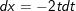
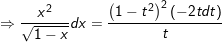
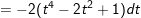
⇒
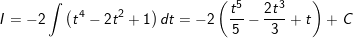
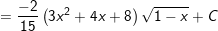
Ví dụ 3: Tính tích phân bất định:
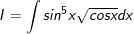
* Lời giải:
- Đặt
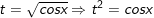
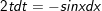
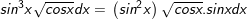
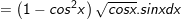
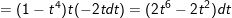
⇒

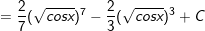
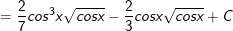
Ví dụ 4: Tìm nguyên hàm:
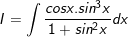
* Lời giải:
- Đặt
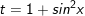
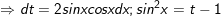
- khi đó:
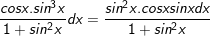
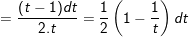
⇒
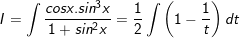
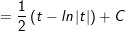
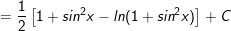
Ví dụ 5: Tìm nguyên hàm của
* Lời giải:
- Đặt
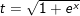
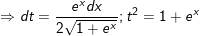
- khi đó:
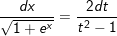
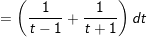
⇒
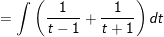
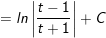
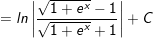
Ví dụ 6: Tính tính phân bất định

* Lời giải:
- Đặt
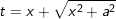
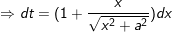
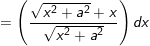
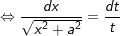
- lúc đó: I
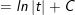
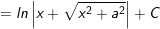
Ví dụ 7: tìm kiếm nguyên hàm của
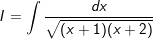
* Lời giải:
- Ta xét 2 trường hợp:
+ TH1:
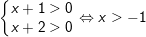
- Đặt

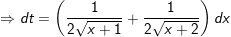
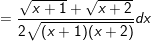
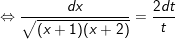
- khi đó:
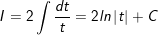
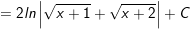
+ TH2:
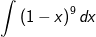
b)

c)
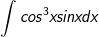
d)
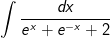
* Lời giải Bài 3 trang 103 sgk giải tích 12:
a) Đặt
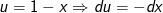
- Ta có:
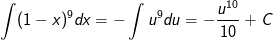
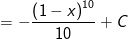
b) Đặt
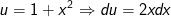
- Ta có:

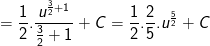
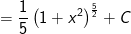
c) Đặt
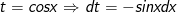
- Ta có:
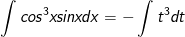
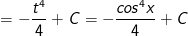
d) Đặt
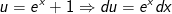
- Ta có:
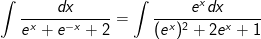

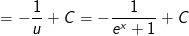
Hy vọng với bài viết về cách search nguyên hàm bằng phương thức đặt biến hóa số và bài bác tập áp dụng có lời giải sinh hoạt trên hữu ích cho những em. Mọi vướng mắc và góp y những em sung sướng để lại phản hồi dưới nội dung bài viết để hoanglamcm.net ghi nhận cùng hỗ trợ, chúc những em học hành tốt.











